Траектория центра движущейся окружности парабола. Таким образом, парабола это множество центров окружностей, касающихся данного круга и данной прямой, касающейся этого круга.
Мультфильм показывает, как это выглядит в движении.
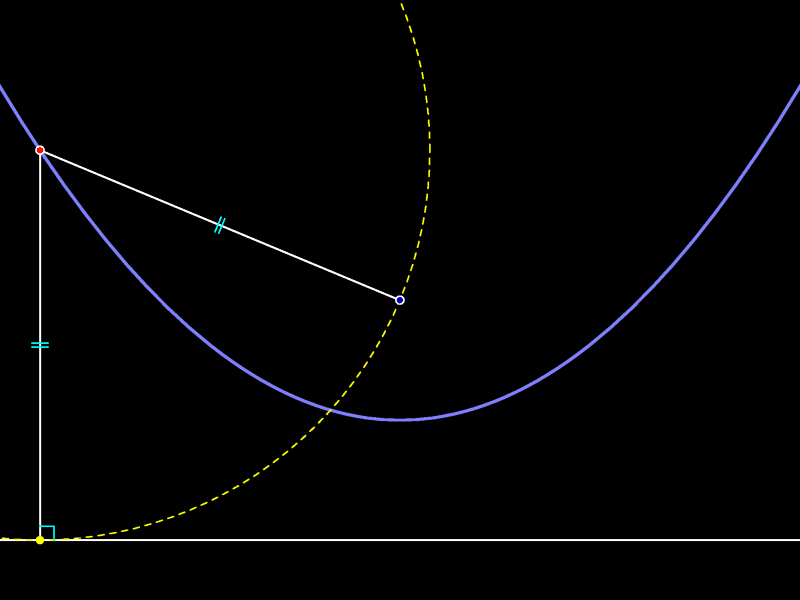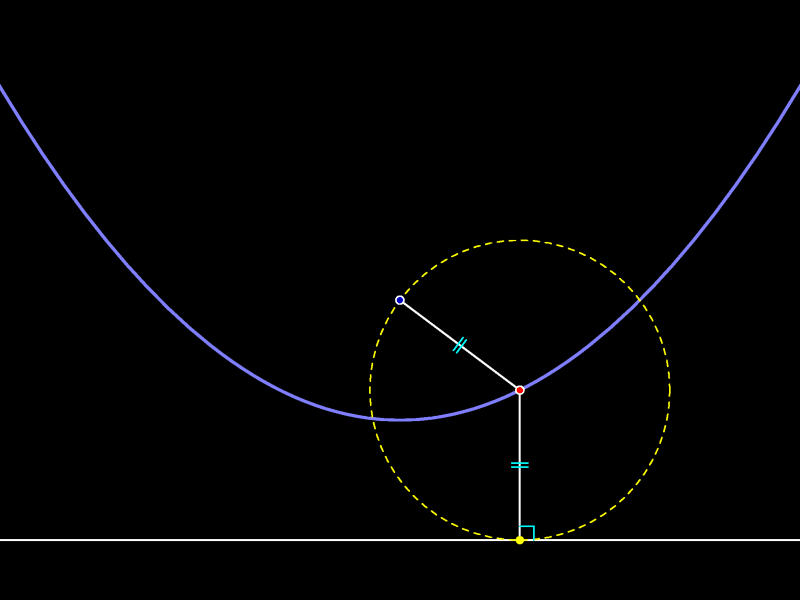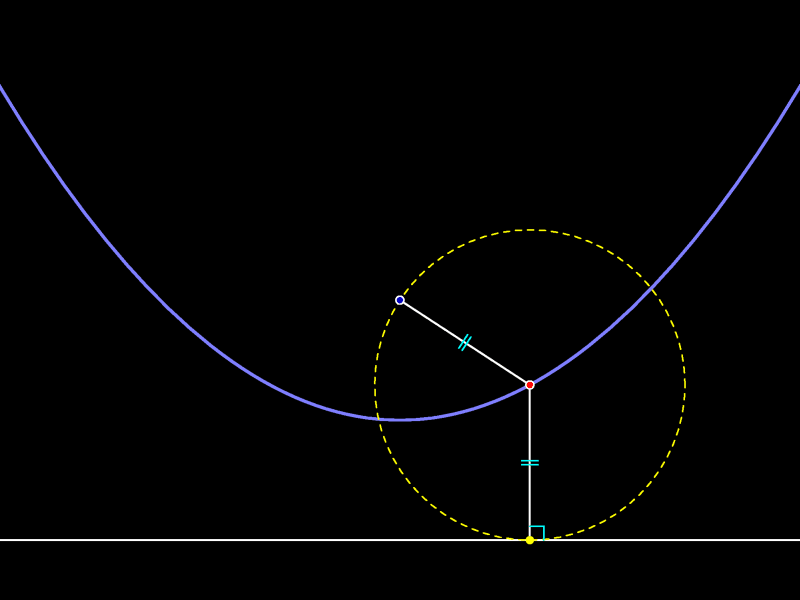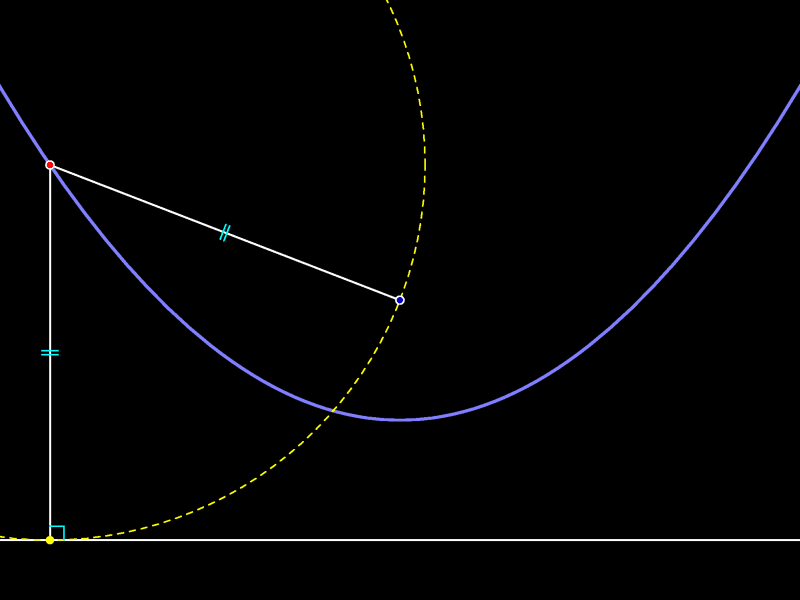
Центр красной окружности равноудалён от центра круга и только что проведённой прямой.
Построим прямую, параллельную данной и расположенную с другой стороны, чем круг, причём так, чтобы расстояние между прямыми равнялось радиусу круга.
Существует бесконечно много окружностей, касающихся прямой и круга.
Геометрическое определение параболы можно сформулировать чуть иначе. Рассмотрим прямую и касающийся этой прямой круг.
Конечно, это парабола! Несложным вычислением можно доказать, что изучаемое в курсе алгебры определение параболы как графика квадратичной функции равносильно геометрическому определению: парабола это множество точек, равноудалённых от данной прямой (директрисы параболы) и не лежащей на директрисе данной точки (фокуса параболы).
Догадайтесь, по какой траектории движется центр окружности!
Поскольку изображённые на рисунке радиусы окружности равны, центр любой такой окружности равноудалён от прямой и точки. Разумеется, верно и обратное утверждение: любая точка, равноудалённая от данной прямой и данной точки, является центром окружности, проходящей через данную точку и касающейся данной прямой.
Существует бесконечно много окружностей, проходящих через данную точку и касающихся прямой.
Рассмотрим произвольную прямую и точку, не лежащую на ней.
Комментариев нет:
Отправить комментарий